一体化伺服电机中的PMSM参数识别

Jia Li

引言

永磁同步电机 ( PMSM ) 因其高效率、高功率密度和出色的机械动力性能而在业界广泛应用。磁场定向控制 (FOC) 常被用于驱动PMSM ，用来改善其动态响应并充分发掘电机的全部潜力。其矢量控制涉及多种环路，包括电流环路以及机械、电气、速度和位置环路。要实现具有最佳性能的控制设计，通常需要精准的电机参数来为 PMSM 控制系统构建恰当的数学模型。

尽管PMSM产品可能附带数据手册，但即使提供，通常也不能涵盖每台电机遇到的运行条件。本文将介绍一种识别PMSM参数的方法，通过使用电机控制模块这种简单的方法来获取精确的电机参数。电机控制算法应基于递归最小二乘 ( RLS ) 法，并带遗忘因子，以实时修改并监测PMSM的变化。

PMSM的磁场定向控制 (FOC)

FOC 的基本思想是能够分别控制场通量和扭矩，类似于直流电机的控制方式。根据 Clarke 和 Park 变换，可根据以下公式（公式1、2、3和4）来计算同步旋转 Q-D 框架下的PMSM模型：

$$v_{QS}=r_S+ω_Rλ_{DS}+ρλ_{QS}$$
$$v_{DS}=r_{S}-ω_rλ_{QS}+ρλ_{DS}$$
$$λ_{QS}=L_Si_{QS}+L_Mi_{QR}$$
$$λ_{DS}=L_Si_{DS}+L_M i_{DR}$$

其中，下标Q和D分别代表Q轴和D轴变量，L_S为电机自感，L_M为电机互感。

为了进一步简化控制，转子磁通应与 D 轴对齐，Q 轴上的转子磁通为零。Q 轴和 D 轴磁通可分别通过以下两个公式（公式5和6）来估算：

$$λ_{QS}=L_Si_{QS}$$
$$λ_{DS}=L_Si_{DS}+λ_M^{'}$$

电磁扭矩可采用以下公式（公式7）来计算：

$$T_E= \frac {3} {2} \frac {P}{2} (λ'_{M}i_{QS} + (L_{D} - L_{Q}) i_{DS}i_{QS}) $$

根据上述方程的变换步骤，磁通量可通过 D 轴电流直接控制。在保持 I_DS 恒定的情况下，扭矩 (T_E) 可以通过调节 Q 轴电流直接控制。如果 I_DS = 0，则电磁扭矩与 I_QS成正比。

利用上述推导过程，可得到PMSM的 FOC原理图 （见图 1）。

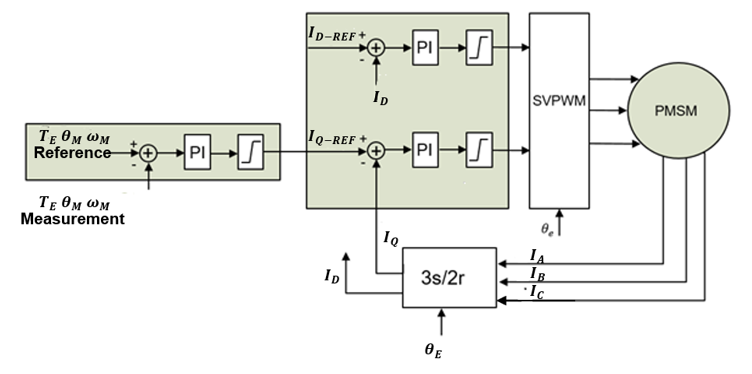
图 1： PMSM矢量控制

外环参考可以是期望扭矩、电机速度或特定的轴位置。将外环参考与测量变量进行比较，并将误差反馈给控制器（以 PI 控制器最为常见）以生成指令扭矩电流 (I_Q-REF)。

D 轴电流参考 (I_D-REF) 可根据磁通量要求设定。电流调节器/控制器的输出 (V_Q-REF 和 V_D-REF) 是空间矢量PWM ( SVPWM )的输入。SVPWM模块会生成逆变器的栅极信号以驱动PMSM 。

电机控制模块可以提供具有自调谐功能的受控参数，以实现PMSM伺服电机所需的动态性能。根据给定的带宽要求，电机控制模块可自动调节每个 PI 控制器。

对于电流环路，开环传递函数可以通过以下公式（公式8）估算：

$$G = \frac{KPS+K1} {S} \frac {1}{L_{S}S + r_S}$$

假设电流带宽为 S = jω，则可根据定子电阻和电感反向计算PMSM的控制参数（KP和 KI）。

与电流环路类似，外环（机械环）开环函数可采用以下公式（公式9）计算：

$$G = \frac{KPS+K1} {S} \frac {kt}{JS + B}$$

其中，kt为电机扭矩常数，J为惯量，B为摩擦系数。

通过上式，根据电机扭矩常数（kt）、惯量（J）和摩擦系数（B）可计算出外环的控制参数。

递归最小二乘法

递归最小二乘法 ( RLS ) 是最小二乘 (LS) 回归算法的递归应用。其每次迭代都会获取新的数据来修改系统之前的估算。

系统输出(y(t))可通过下式（公式10）计算：

$$y(t)=ϕ^T (t)θ(t)$$

其中 ϕ 为系统输入矩阵，θ 为PMSM系统参数。

用 $$\hatθ$$ 表示估算的系统参数。目标函数，即要最小化或最大化的项，可以通过下式 （公式11）来估算：

$$J(θ,t)= \frac {1}{2} ∑_{i=1}^t(y(i)-\phi^T (i) \hatθ (i)) $$

新的 P 和 L 矩阵可分别通过下面的两个公式（公式12和13）来计算：

$$P^{-1} (t)=∑_{i=1}^t\phi(i)\phi^T(i)$$ $$L(t)=P(t)\phi(t)$$

递归最小二乘参数识别方案通过以下公式（公式14、15、16、17和18）来估算：

$$ϵ(t)=(y(t)-\phi^T (t)) \hatθ (t-1)$$
$$L(t)=P(t-1)\phi(t) (I+\phi^T (t)P(t-1)\phi(t))^{-1}$$
$$P(t)=(I-L(t)\phi^T (t))P(t-1)$$
$$\hatθ(t)=\hatθ (t-1)+L(t)ϵ(t)$$
$$t=t+1$$

在算法中添加遗忘因子可使方案具备处理时变系统的能力。遗忘因子数据的权重取决于数据有多旧；数据越旧，对当前迭代的影响就越小。最新的数据则被赋予最大的权重。遗忘因子 (λ) 在 [0,1] 之间取值。新目标函数可以通过以下公式（公式19）来估算：

$$J(θ,t)=\frac {1}{2} ∑_{i=1}^tλ^{t-i} (y(i)-\phi^T (i)\hat θ (i)) $$

根据上式中的新目标函数，第 n 旧的数据权重为 λⁿ。带遗忘因子的递归最小二乘法可以通过以下公式（公式20、21、22、23和24）来计算：

$$ ϵ(t)=(y(t)-\phi^T (t)) \hatθ (t-1)$$
$$L(t)=P(t-1)\phi(t) (λI+\phi^T (t)P(t-1)\phi(t))^{-1}$$
$$P(t)= \frac {1}{λ}(I-L(t) \phi^T (t))P(t-1)$$
$$\hatθ (t)=\hatθ (t-1)+L(t)ϵ(t)$$
$$t=t+1$$

实验结果

我们通过MMS757188-36-R1-1来验证结果。表 1 列出了其数据手册中的参数。

表 1：电机参数

定子相电阻	300mΩ
定子相电感	350µH
电机惯量	410gxcm2
扭矩常数	57mN x m/A
极对数	4

图 2：EZmotion电机（MMS757188-36-R1-1）

首先为电机参数设置初始起点为 [0 0 0 0 0]^T ，具体参数包括：相电阻 (R_S)、Q 轴电感 (L_Q)、D 轴电感 (L_D)、扭矩常数 (kt) 和电机轴惯量 (J)。

对于RLS算法，设置初始P矩阵为 P = 10000 x I_{5 x 5}，遗忘因子设置为λ = 0.99。

将启动条件应用到电机控制模块，以执行RLS电机参数算法。硬件实验结果如图3-图7所示。

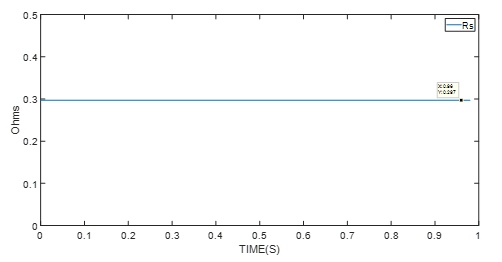
图3 电阻识别实验结果

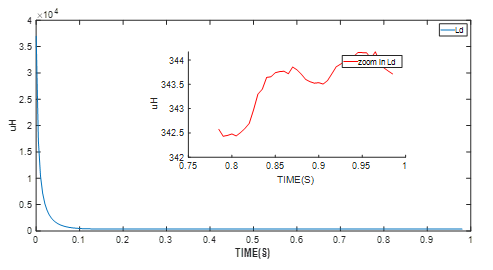
图4：D轴电阻识别实验结果

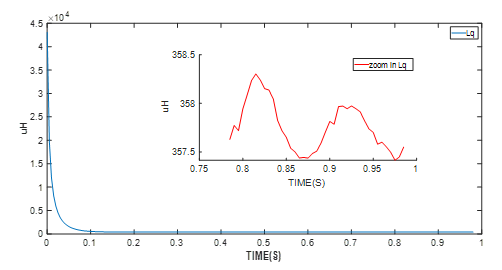
图5：Q轴电阻识别实验结果

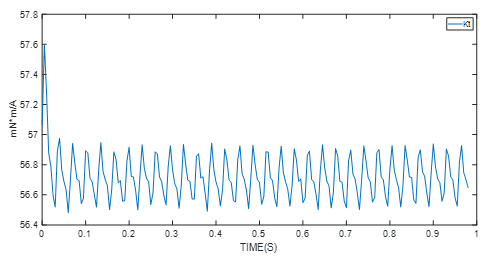
图6 扭矩常数识别实验结果

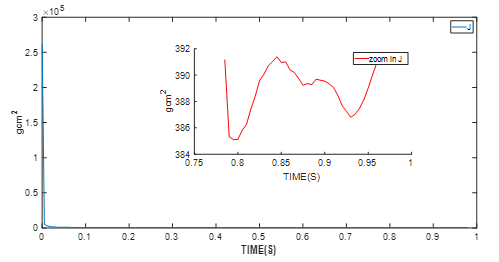
图7：轴惯量识别实验结果

电机控制模块（本例中为MMS757188-36-R1-1）还可检测参数识别算法是否已进入稳定阶段。当算法进入上图所示的稳定状态后，将采用最终值；最终值为平均电机参数值。

表 2：识别出的电机参数

定子相电阻	297mΩ
D 轴电感	343µH
Q 轴电感	358µH
电机惯量	390gxcm2
扭矩常数	57mNxm/A
极对数	4

控制回路自调谐

如上节所述，电机参数会影响PMSM的 FOC 控制参数。为了帮助工程师实现所需的电机性能，控制套件中配备了一个电机控制模块，该模块通过公式8和公式9中得到的系统传递函数自动调谐控制参数。如果电机参数可用，则工程师只需通过 GUI 输入每个环路所需的带宽。主计算机将计算电机的控制参数，然后将控制参数更新到电机中，从而确保电机性能。

PMSM控制传递函数高度依赖于电机参数。如果电机参数不正确，电机将无法有效运行。下面我们将通过改变轴惯量 (J)进一步探讨这个问题。

PMSM经常被用作高性能伺服电机，其工作条件因情况而异。工程师可能有准确的电机参数数据手册，也可能需要手工测量电机参数。然而一旦电机被置于复杂的机械系统中，其轴惯量就很难确定。

MMS757188-36-R1-1可用于驱动旋转盘（见图 8）。旋转盘将轴惯量从410gxcm2增加到7100gxcm2 。FOC设计具有20Hz的位置带宽、 200Hz的速度带宽和2000Hz的电流带宽。

图 8：电机驱动旋转盘

如果所用电机参数来自电机数据手册，则自动调谐算法会使用预期的环路带宽和错误的电机参数来设计控制环路，因为数据手册仅提供空载惯量。位置参考信号为斜坡信号，其斜率为10rad/s。如图 9 所示，当位置环路失控时，位置反馈会出现较大的振荡。

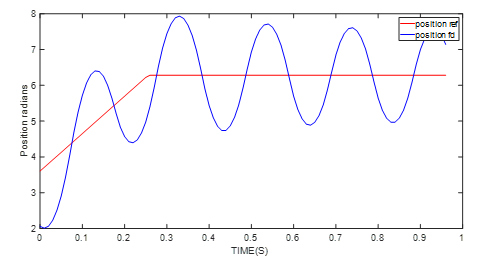
图 9：原始 J 值的位置控制性能

我们再通过电机控制模块来运行参数识别算法。电机参数被更新为电机当前的工作条件，自调谐算法会帮助工程师根据当前工作条件下的电机参数调节控制回路。仍采用相同的位置参考。如图10所示，位置反馈追随参考信号，误差稳定在 0.03%左右。

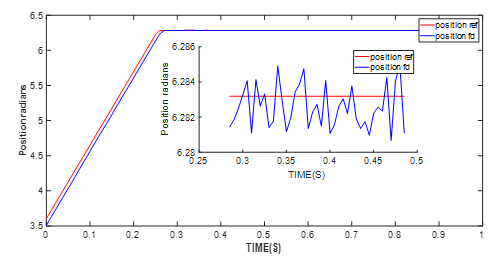
图 10：更新 J 值后的位置控制性能

结语

本文介绍了一种通过电机控制模块、并基于RLS对PMSM进行电机参数识别的解决方案。通过对MMS757188-36-R1-1进行硬件实时测试，验证了该方案的性能。文中还通过不同惯量值的位置控制示例说明了参数识别的重要性。此外，由于PMSM FOC 依赖于多个电机参数，本文亦演示了其他参数对控制环路的影响。